IBM Thinkpad 600E bios mod for processor update

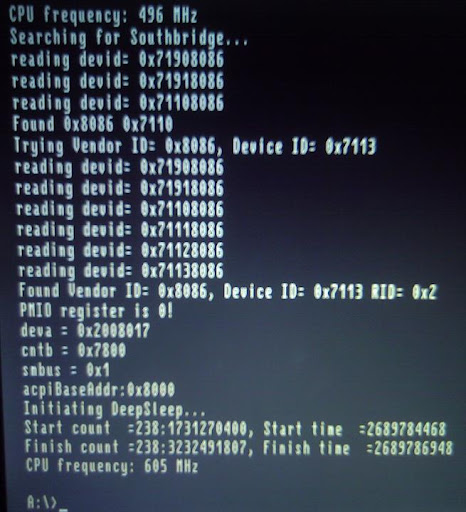
Ok I took a picture of what happens when running dsleep.exe in debug mode




I didn't find any debug file so I thought hte pic would help a bit!

When I restart nothing changes! cpu is back to 500MHz

Here is the link itself:
http://lh5.google.com/image/redscorpion ... psleep.jpg

I dunno sometimes why the image itsel doesn't show on the page of this site!

Sorry, was not able to see the picture

"Your client does not have permission to get URL /1.1 from this server."

Here:

http://picasaweb.google.com/redscorpion78/Deepsleep

Sorry for the problem, it was working when I posted it!

Hi.

Thanks to Sharedoc and all other people who have helped to gather this information and experience together. I've just successfully upgraded my Thinkpad 600E with a 750Mhz PIII running at 600 Mhz (didn't want to risk anything by trying hardware mod...). Before swapping the cpu I edited the bios (and actually had to do all the calculations again lol: there was "22" at 0x20... I put in "2A" and it worked fine ), so the boot with the new cpu was error-free. Next, I booted into linux and after compiling deepsleep kernel module I loaded it and voilá, the l2-cache was activated. I then went on to playing a dvd as a test and was very happy with the result: great performance.
Now, I have got a problem, and that's mainly the reason for posting here now: as I do Audio-work (I am a musician), I need low latency, so I have my machine configured with a dual boot: one is the stock 2.6.18.1 kernel, the other one is the patched (with realtime-preempt patches from Ingo Molnar) 2.6.19 kernel. The deepsleep kernel module works great under 2.6.18.1, but fails completely under the other kernel: it just freezes the laptop! I have to use the power switch to reboot it!
I actually found another kernel module which seems to rely on the same code from linuxbios, and it had exactly the same effect: complete freeze under the RT-enabled kernel. Then I tried something completely crazy (which obviously turned out to not work at all): I set up a clean (stock) kernel source tree of 2.6.19, copied missing files from the 2.6.19-rt tree into it (as I didn't want to build a kernel just for trying something that maybe not work at all) and then compile the deepsleep module against that tree. It actually modified its behavior: it loaded ok, didn't freeze anything, but it simply did NOTHING... not even a line in dmesg...

So, I am kind of stuck here, as I really need Realtime kernel for my audio work (which obviously leads me nowhere without the l2cache )... I don't know if it's worth bothering Ingo Molnar about this, because I suspect he won't know how to deal with this (since when is there a connection between Realtime scheduling and low level processor register manipulation? )
So, the only other solution I found was a hacked GRUB (including l2cache and deepsleep stuff) that somebody managed to do, but I feel a little strange about trying that out (first, I never installed grub, and it seems quite a bit more complicated than lilo , and if using that version, I wouldn't be able to update grub in future, unless it would be patched again - and I don't even know if his website is still mantained...).
But well, I think that this would do it, as it does it's trick before loading the kernel (supposing that this modified grub doesn't bring me other problems...).

So, what I would really like to find is a simple and neat tool (if necessary as a module, that's ok) that sets the necessary registers in order to activate the l2 cache and does NOT rely on scheduling and whatever related stuff (so that it doesn't crash with the RT-kernel). Here I was thinking of direct and dirty hardware access, I actually found something like that when googling around, but I am afraid it could not be ok for the PIII? I would even have the will to try it, but the problem is implementation: I have very little C knowledge (the only language I know quite well is Pascal and assembly, although I never did anything with x86 cpus...). Anyway, maybe someone interested in helping me to play around with this, so here is what I found: http://www.cs.helsinki.fi/linux/linux-kernel/2003-08/1019.html
And this here also gave me an idea (stealing code from memtest86 lol):
http://mail.nl.linux.org/kernelnewbies/2006-03/msg00132.html but obviously that would have to be the opposite action

So, whatever I'd apreciate any suggestions or help.

P.S.:
I did not disable the on board memory in bios, as I was curious to see how they would behave (read that some people didn't have problems with them enabled), and at least until now eveything is working just fine! Since installing the pIII cpu, I had the laptop already running for about 2 hours straight and did at least 10 boots (as deepsleep kept crashing lol) and nothing weird happened, everything 100%.

P.S.2: just a little off-topic here: the PIII 750Mhz cpu I have, I got it for a nice price from ebay from a guy in the United States, because here in europe (I am living in Portugal) I didn't find anything, and I nearly had a heart attack (joking ) when I received the package: it was a simple USPS Priority mail envelope! The cpu was in it without any protection, NOTHING...! but to my great, great relief it survived this dangerous trip without any damages.. a little miracle lol... but this also shows us how good the build quality of those processors is...

I don't know Linux yet, so I don't know if this will be any help, but here's a link to someone else's L2 cache enabler for Linux:
Activating the L2 data cache of Pentium III in Thinkpads 600

I've never used it, have no idea if it works, all I did was bookmark it.

Phil.

Solved
Turned out to be a problem related to kernel config and/or realtime patch, what I did was update to 2.6.20, apply realtime patch, reconfigure kernel (I noticed I had the processor type wrong in the old kernel (PII instead of PIII), and from then on it worked flawlessly!

Perhaps I'm blind, but I can not find a how-to for the 100 MHz FSB mod.. all I find is 108. Is there a 100 MHz mod?

Is there a 100 MHz mod?

No. The PIII has a 100MHz FSB, so no mod is required. Maybe you are looking at your original PII which runs at 66MHz? Most of this thread concentrates on installing and modding a new PIII CPU, not working with your original PII.

Phil.

Is there a 100 MHz mod?

No. The PIII has a 100MHz FSB, so no mod is required. Maybe you are looking at your original PII which runs at 66MHz? Most of this thread concentrates on installing and modding a new PIII CPU, not working with your original PII.

Phil.

Yeah.. I did a bit more reading and found out it wasn't easily possible. Can I still do the 8% mod the PIII guys are using for 108 MHz? What would that result for FSB on the PII? Does it at 8 MHz or 8% of the current clock? If it would add 8 MHz to my FSB resulting in 74 MHz I would be happy with that for now?

Xylene: PII at higher FSB? I don't know if it's possible, but one thing I'm sure: you won't be happy with it... much easier is it to simply upgrade to a PIII (even if just a 500 or 600), do no mods at all and you'll have more gain in speed than with any PII even with whatever you did to tune it... Believe me, the difference is radical, not so much because of the more Mhz, but because of more instruction sets (SSE i.e.) and better implementation of the PIII, aswell as running on 100MHZ FSB. So I'd recommend you to get a PIII on ebay and see for your own how dramatic the improvement is. And if you really want to max it out (without getting into trouble with heat) get a 750 or 800mhz one, and let it run in slow mode (which it will do by default, unless you do the speedstep mod) and you'll have a huge improvement in performance for the minimum of work (only things you have to do is disable L2 cache in BIOS (instructions provided in this thread and on several websites), and then get a software tool to re-enable it at runtime (exists for both windows and linux). That's it. It's what I did and for most people this should be enough. If you happen to still want more and are adventurous enough and have required skills, you can do the mods presented here.

Xylene,

As far as I remember, the 8% FSB mod works for PII as well.

My thanks to everyone who's contributed here. With the advice I found here, it was easy to drop a PIII 500mhz into my 600e (2645-4AU), and it only cost me $12.00 on e-bay. Can't beat the price for performance gain on that one. Plus, it helped feed my tinkering obsession.

Couple questions:

1. For the moment, I'm running only Win2K with L2 cache enabled through the PowerLeap Cache Config Tool mentioned by Holgi128 on page 12 of the string (cacheutility.zip) . I couldn't get the PoweLeap CPU Control Panel to install, it kept giving "An error occurred during the move data process". I know someone else reported that error somewhere but I can't find where. Do I need to keep trying to get the Control Panel app to install? Cache Config appears to be enabling cache on each restart according to CPU-Z, but the L2 latency reported by the Latency.exe tool is "7". Is it supposed to be that high?

2. For future Linux installs (dual boot) I thought I'd try the GRUB mod mentioned here that apparently works with Linux and Windows. I'm assuming that if I can get that to run, I wouldn't have to worry about the PowerLeap apps at all?

3. I know some folks have removed their modems. At this point, mine is just making heat and stealing resources. I assume its just a matter of pulling it? I'd be reinstalling the OS fresh after doing so. Any advice on how to cover the resulting hole to keep foreign objects (like pens launched by my 4 year old) out of it? I also assume that there's no other hardware available (like a NIC) that can plug into the same socket?

Thanks again to all for helping relative Noobs like myself.

mark

1. For the moment, I'm running only Win2K with L2 cache enabled through the PowerLeap Cache Config Tool mentioned by Holgi128 on page 12 of the string (cacheutility.zip) . I couldn't get the PoweLeap CPU Control Panel to install, it kept giving "An error occurred during the move data process".

I've seen this problem reported over on the Thinkpads Forum with Powerleap CPU Control Panel before, but I don't know where it comes from: Power Leap Utility Installation Problem.

Do I need to keep trying to get the Control Panel app to install? Cache Config appears to be enabling cache on each restart according to CPU-Z, but the L2 latency reported by the Latency.exe tool is "7". Is it supposed to be that high?

There should be no problem with using the Powerleap Cache Utility instead of the Powerleap CPU Control Panel to enable the L2 cache. I use the cache utility on my 770Z upgraded to PIII 500MHz. And my impression is that the Powerleap Cache utility is actually slimmer and requires less overhead than the CPU Control Panel anyways. Though admitedly, I don't know anything about this latency=7.

Phil.

Hello to you guys.
First of all, thank you for all the good information here.
I have some questions about mods done (or tried) by serveral people in this thread.

At first, I have some questions about setting CAS-latency 3.
I want to try this on a 770x and was already able to change the RAS-to-CAS delay and the RAS precharge time with the tool wpcredit 1.4. This tool can view & edit the Chipset register for the PCI-Host-Bridge in real-time under windows.
But if I change the CAS-Latency bit the system freezes. I need to modify the BIOS so CAS latency 3 is set when the thinkpad is powered on. When I open the BIOS-Editor with ctrl-d and change the related byte 4 in the third line ("extended CMOS (first 64 bytes)", I think) from value 04 to 00, hit F2 and power off + on again the change is not applied which also happened on Sharedocs 600e.
So it is necessary to edit the BIOS file and flash it.
With the bios1351-tool mentioned in the first pages of this thread I got the bios dump file and I can open it with a hex-editor. But if I can find and edit the byte (have not searched for it yet) can I simply flash the modified BIOS file? What program and what file extension would I have to use?
And if it is not that simple, does anyone of you have any ideas how I can recompress the file to this IBM format (.fl1 , .fl2) for flashing it with the normal IBM flash-utility or do you think this is not possible anyway?

Then I need more information about building a turbo-pll into the Thinkpad.
The usual methode is to change the crystal on the motherboard and to feed the right clocks for USB (48Mhz), I/O (24Mhz), AGP(66Mhz) and PCI (33Mhz)with the second pll, am I correct here or did I missunderstood something? If not, can I also use the second pll for just sending the higher FSB to the mainboard? Furthermore, do I also have to connect PWR_DOWN and STPCLK signals to the second oscillator and is the pck2000 device by Philips exactly the same as the SG577DYB by IMI so the Datasheet of the pck2000 could be used? I am going to use a second SG577DYB device so the oscillators would be the same.

And finally I need to know some dimensions and facts about the compaq 610c heatsink used by ChrisL. I also want to use this heatsink in my 770x because the default one is not even able to cool the 850Mhz PIII down in idle for 10 minutes and my self-made one can only cool it down in idle or soft load (everything tested with arctic silver 5). I need to know the thickness of the copper radiator and the fan (it seems to look thinner) and I need to know the length of the whole heatsink. Can the heatpipes be bent gently a bit if necessary?

greetings to you all from el-sahef